What Shape Has Two Sides

Polygon with two sides and 2 vertices

Regular digon
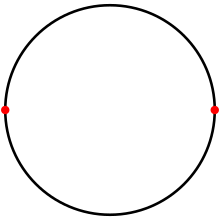On a circumvolve, a digon is a tessellation with ii antipodal points, and ii 180° arc edges.
Type	Regular polygon
Edges and vertices	two
Schläfli symbol	{2}
Coxeter–Dynkin diagrams
Symmetry group	D₂, [2], (*two•)

In geometry, a digon is a polygon with ii sides (edges) and 2 vertices. Its construction is degenerate in a Euclidean aeroplane because either the two sides would coincide or one or both would have to exist curved; nevertheless, information technology can be easily visualised in elliptic space.

A regular digon has both angles equal and both sides equal and is represented by Schläfli symbol {2}. It may be constructed on a sphere equally a pair of 180 degree arcs connecting converse points, when it forms a lune.

The digon is the simplest abstract polytope of rank 2.

A truncated digon, t{2} is a square, {4}. An alternated digon, h{2} is a monogon, {i}.

In Euclidean geometry [edit]

The digon can have one of two visual representations if placed in Euclidean space.

1 representation is degenerate, and visually appears every bit a double-roofing of a line segment. Appearing when the minimum distance between the 2 edges is 0, this grade arises in several situations. This double-covering class is sometimes used for defining degenerate cases of another polytopes; for instance, a regular tetrahedron can exist seen as an antiprism formed of such a digon. Information technology can be derived from the alternation of a square (h{4}), every bit it requires two opposing vertices of said square to exist connected. When college-dimensional polytopes involving squares or other tetragonal figures are alternated, these digons are usually discarded and considered single edges.

A 2nd visual representation, infinite in size, is as two parallel lines stretching to (and projectively coming together at; i.e. having vertices at) infinity, arising when the shortest distance between the 2 edges is greater than zero. This form arises in the representation of some degenerate polytopes, a notable example existence the apeirogonal hosohedron, the limit of a general spherical hosohedron at infinity, composed of an infinite number of digons meeting at two antipodal points at infinity.^[1] All the same, as the vertices of these digons are at infinity and hence are not leap by closed line segments, this tessellation is normally not considered to be an additional regular tessellation of the Euclidean plane, even when its dual lodge-two apeirogonal tiling (infinite dihedron) is.

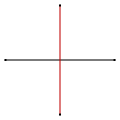
A chemical compound of ii "line segment" digons, every bit the two possible alternations of a square (note the vertex arrangement).
The apeirogonal hosohedron, containing infinitely narrow digons.

Any straight-sided digon is regular even though it is degenerate, considering its ii edges are the same length and its two angles are equal (both being zero degrees). Every bit such, the regular digon is a constructible polygon.^[2]

Some definitions of a polygon do not consider the digon to be a proper polygon because of its degeneracy in the Euclidean case.^[3]

In elementary polyhedra [edit]

A nonuniform rhombicuboctahedron with blueish rectangular faces that degenerate into digons in the cubic limit.

A digon as a face of a polyhedron is degenerate because it is a degenerate polygon. But sometimes information technology can have a useful topological existence in transforming polyhedra.

As a spherical lune [edit]

A spherical lune is a digon whose two vertices are converse points on the sphere.^[iv]

A spherical polyhedron constructed from such digons is called a hosohedron.

A lune on the sphere.
Six digon faces on a regular hexagonal hosohedron.

Theoretical significance [edit]

The digon is an of import construct in the topological theory of networks such as graphs and polyhedral surfaces. Topological equivalences may be established using a procedure of reduction to a minimal set up of polygons, without affecting the global topological characteristics such as the Euler value. The digon represents a phase in the simplification where information technology can be simply removed and substituted by a line segment, without affecting the overall characteristics.

The cyclic groups may exist obtained equally rotation symmetries of polygons: the rotational symmetries of the digon provide the group C₂.

References [edit]

Citations [edit]

^ The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5, p. 263
^ Eric T. Eekhoff; Constructibility of Regular Polygons Archived 2015-07-14 at the Wayback Machine, Iowa Land Academy. (retrieved 20 December 2015)
^ Coxeter (1973), Chapter i, Polygons and Polyhedra, p.4
^ Coxeter (1973), Chapter 1, Polygons and Polyhedra, pages 4 and 12.

Bibliography [edit]

Herbert Busemann, The geometry of geodesics. New York, Bookish Press, 1955
Coxeter, Regular Polytopes (third edition), Dover Publications Inc, 1973 ISBN 0-486-61480-8
Weisstein, Eric Due west. "Digon". MathWorld.
A.B. Ivanov (2001) [1994], "Digon", Encyclopedia of Mathematics, European monetary system Press